三角分布
一直没有听说和使用过三角分布,这里对这个分布做一个简短的介绍。
在概率论与统计学中,三角分布是下限为\(a\),众数为\(c\),上限为\(b\)的连续概率分布。
$$f(x|a,b,c) = \begin{cases} \frac {2(x-a)}{(b-a)(c-a)}, & a \le x \le b \\ \frac {2(b-x)}{(b-a)(b-c)}, & c \lt x \le b \end{cases}$$
通常,如果对考察对象的概率分布所知信息很少,例如仅仅知道最大值与最小值,那么可以使用均匀分布模型。但是,如果已经知道了最可能出现的结果,那么就可以用三角形分布进行模拟。其中三角形可以对称也可以不对称,可以是等腰三角形、直角三角形等。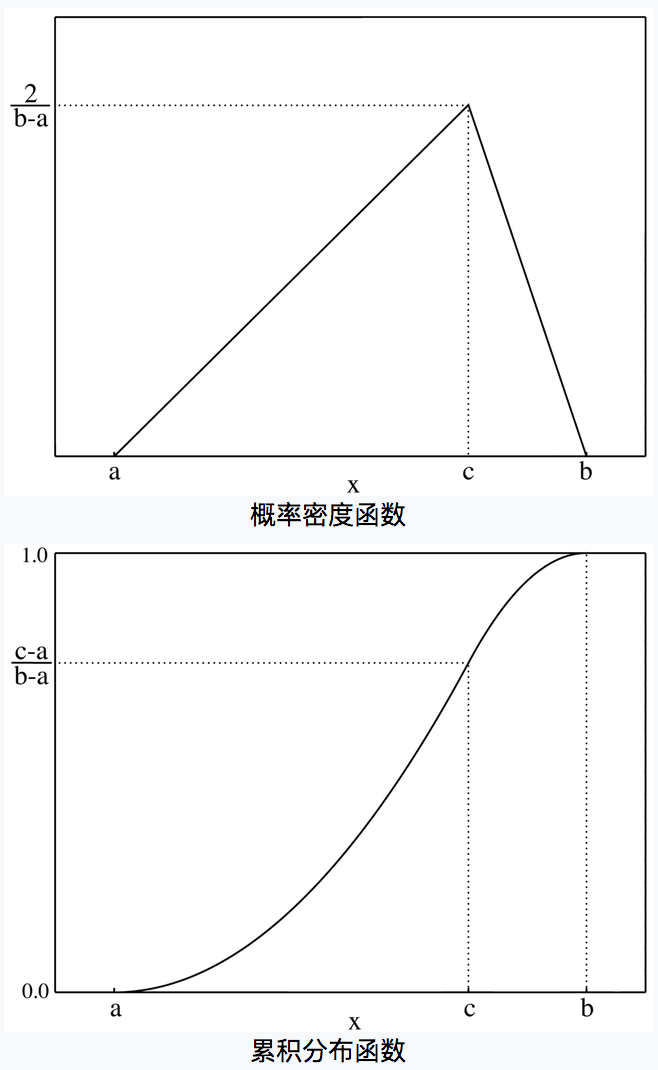
总结
三角分布常用于对业务风险和随机过程建模。例如,难以收集有关新建筑建设费用的数据。但是,可以估计最小值、最大值和最可能(众数)的建设费用。
参考: